SkillWisor

Introduction

Options trading offers significant leverage and strategic flexibility, but comes with complexities. Unlike stocks, options prices are affected by multiple factors beyond just the underlying asset’s price. Options Greeks help us understand these factors and manage risks effectively.

This guide will explain each Greek in simple terms, show how they affect option pricing, and introduce practical hedging strategies.

What Are Options Greeks?

Options Greeks are measurements that show how sensitive an option’s price is to various factors:

• Delta (Δ): How much the option price changes when the underlying asset price changes
• Gamma (Γ): How much Delta changes when the underlying asset price changes
• Theta (Θ): How much the option price changes as time passes
• Vega (ν): How much the option price changes when volatility changes
• Rho (ρ): How much the option price changes when interest rates change

Let’s look at how these Greeks might appear in a typical options chain:

Sample Nifty 50 Options Chain (Spot Price: ₹22,000)

Strike Price	Type	Option Price	IV (%)	Delta	Gamma	Theta	Vega	Rho	Moneyness
21,800	Call	₹300	15.5%	0.75	0.0008	-15.0	12.0	0.08	ITM
21,900	Call	₹220	15.0%	0.65	0.0012	-18.0	11.5	0.07	ITM
22,000	Call	₹150	14.8%	0.50	0.0015	-20.0	11.0	0.06	ATM
22,100	Call	₹100	15.2%	0.35	0.0012	-18.0	10.5	0.05	OTM
22,200	Call	₹60	15.8%	0.25	0.0008	-15.0	10.0	0.04	OTM

Note on Moneyness:

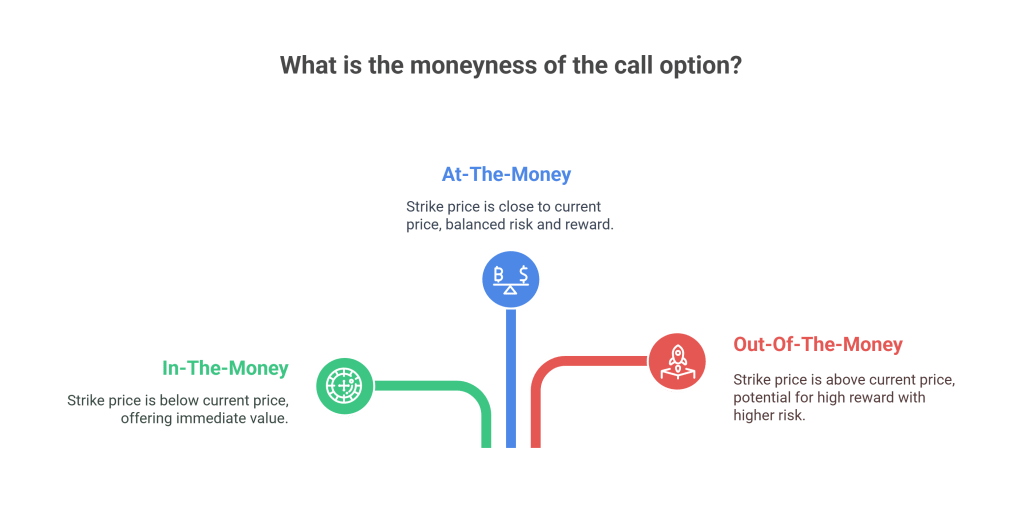
• In-The-Money (ITM): For calls, when strike price is below current price
• At-The-Money (ATM): When strike price is close to current price
• Out-Of-The-Money (OTM): For calls, when strike price is above current price

Understanding Each Greek

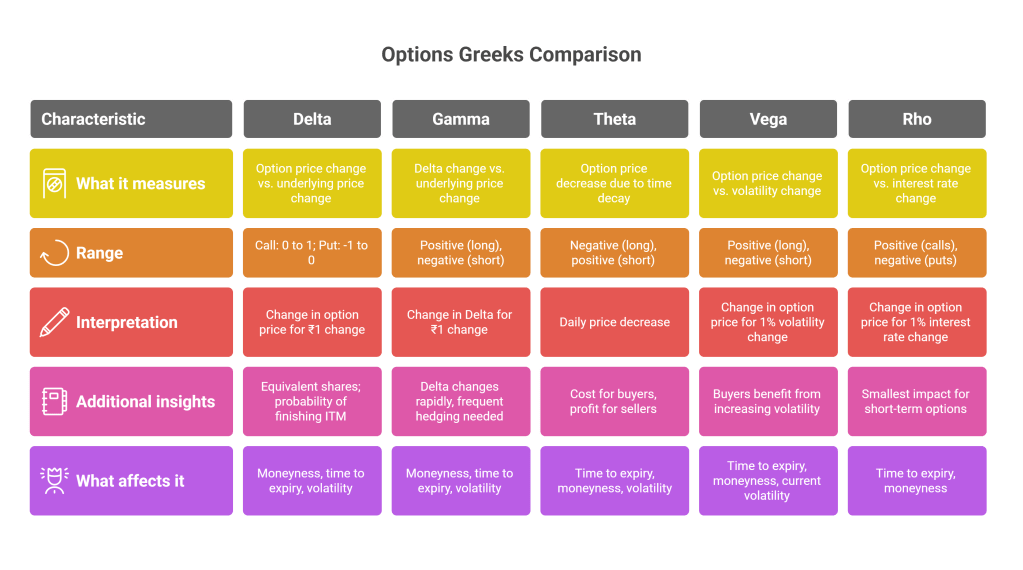
1. Delta (Δ)

What it measures: How much an option’s price changes when the underlying asset price changes by ₹1.

Range:

• Call options: 0 to 1
• Put options: -1 to 0

How to interpret it:

• Delta of 0.50 for a call: If the underlying price increases by ₹1, the option price increases by ₹0.50
• Delta of -0.60 for a put: If the underlying price increases by ₹1, the option price decreases by ₹0.60

Additional insights:

• Delta can be seen as equivalent shares – 10 calls with 0.60 Delta are like owning 600 shares (10 contracts × 100 shares/contract × 0.60)
• Delta roughly estimates the probability of finishing in-the-money

What affects Delta:

• Moneyness: Deep ITM options have Deltas near 1 (calls) or -1 (puts); ATM options have Deltas around 0.50; OTM options have Deltas approaching 0
• Time to expiry: As expiration approaches, Delta becomes more extreme (closer to 0 or 1)
• Volatility: Higher volatility pushes all Deltas toward 0.50

2. Gamma (Γ)

What it measures: How much Delta changes when the underlying price changes by ₹1.

Range: Always positive for long options, negative for short options.

How to interpret it:

• Gamma of 0.0015: If the underlying increases by ₹1, Delta increases by 0.0015

Additional insights:

• High Gamma means your Delta changes rapidly, requiring frequent hedging
• Low Gamma means your Delta is more stable

What affects Gamma:

• Moneyness: Highest for ATM options, approaches 0 for deep ITM/OTM
• Time to expiry: Highest for ATM options near expiration
• Volatility: Higher volatility generally leads to lower Gamma

3. Theta (Θ)

What it measures: How much an option’s price decreases each day due to time decay.

Range: Typically negative for long options, positive for short options.

How to interpret it:

• Theta of -20: The option price decreases by ₹20 each day, all else being equal

Additional insights:

• For option buyers: Theta is a cost of holding the position
• For option sellers: Theta is a source of profit

What affects Theta:

• Time to expiry: Accelerates as expiration approaches (especially in the last 30-45 days)
• Moneyness: Highest for ATM options
• Volatility: Higher volatility generally leads to higher Theta

4. Vega (ν)

What it measures: How much an option’s price changes when implied volatility changes by 1%.

Range: Always positive for long options, negative for short options.

How to interpret it:

• Vega of 11: If implied volatility increases by 1%, the option price increases by ₹11

Additional insights:

• Option buyers benefit from increasing volatility
• Option sellers benefit from decreasing volatility

What affects Vega:

• Time to expiry: Highest for long-dated options, approaches 0 near expiry
• Moneyness: Highest for ATM options
• Current volatility level: Impact changes based on current volatility levels

5. Rho (ρ)

What it measures: How much an option’s price changes when interest rates change by 1%.

Range:

• Typically positive for calls
• Typically negative for puts

How to interpret it:

• Rho of 0.06 for a call: If interest rates increase by 1%, the option price increases by ₹0.06

Additional insights:

• Generally has the smallest impact among Greeks for short-term options
• More significant for long-dated options (LEAPS)

What affects Rho:

• Time to expiry: Higher for long-dated options
• Moneyness: Generally higher for ITM options

How Greeks Affect Option Pricing

Delta: The Price Driver

• Primary factor in short-term price changes
• Total Delta exposure in your portfolio indicates directional risk
• Example: If your portfolio has a net Delta of 500, it’s equivalent to owning 500 units of the underlying

Gamma: The Delta Accelerator

• Shows how quickly your directional exposure (Delta) changes
• Long Gamma positions benefit from large price swings
• Short Gamma positions benefit from stable prices
• High Gamma means more frequent portfolio rebalancing is needed

Theta: The Time Eroder

• Reflects the predictable erosion of option value over time
• Options near expiration lose value faster (the “Theta cliff”)
• Option buyers need significant price movement to overcome Theta
• Option sellers profit from Theta decay

Vega: The Volatility Amplifier

• Significant changes in implied volatility can dramatically affect option prices
• Volatility often increases before major events and decreases afterward
• Long options benefit from volatility increases
• Short options benefit from volatility decreases

Rho: The Interest Rate Factor

• Typically has minor impact for short-term retail traders
• More important for long-dated options or large institutional portfolios
• Higher interest rates generally benefit call options and hurt put options

Practical Hedging Strategies

Delta Hedging

Goal: Neutralize directional risk by making your portfolio insensitive to small price movements.

How to implement:

1. Calculate net Delta across all positions
2. Take opposite position in the underlying to offset
3. For positive Delta: sell the underlying
4. For negative Delta: buy the underlying

Example:

• You have 1 Nifty 50 call option (lot size 50) with Delta of 0.60
• Delta exposure = 0.60 × 50 = 30
• To hedge: Sell 30 units of Nifty 50 futures

Challenges:

• Requires frequent rebalancing (especially with high Gamma)
• Transaction costs add up
• Large price moves can cause significant rebalancing losses

Gamma Hedging

Goal: Stabilize your portfolio’s Delta to reduce the need for frequent rebalancing.

How to implement:

1. Calculate net Gamma
2. To reduce positive Gamma: Sell options (especially ATM)
3. To reduce negative Gamma: Buy options (especially ATM)
4. Re-adjust Delta afterward

Challenges:

• Adds complexity
• Can be expensive (buying options adds Theta cost)
• Changes other Greeks (especially Vega)

Theta Strategies

Positive Theta strategies (collecting time decay):

• Covered calls: Sell calls against stock you own
• Cash-secured puts: Sell puts with cash set aside to buy stock
• Credit spreads: Sell higher-premium option, buy lower-premium option
• Iron condors: Combine bull put spread and bear call spread
• Short straddles/strangles: Sell both calls and puts

Negative Theta strategies (paying for time decay):

• Long calls/puts: Buy for strong directional views
• Long straddles/strangles: Buy both calls and puts for volatility or large moves
• Calendar spreads: Sell near-month option, buy same-strike further-month option

Vega Hedging

Goal: Neutralize exposure to volatility changes.

How to implement:

1. Calculate net Vega
2. To reduce positive Vega: Sell options (especially long-dated ATM)
3. To reduce negative Vega: Buy options (especially long-dated ATM)
4. Consider VIX products for broad market volatility hedging

Important during:

• Earnings announcements
• Economic reports
• Geopolitical events
• Any period of expected volatility change

Practical Considerations

Model Limitations

• Greeks are theoretical values based on pricing models (mainly Black-Scholes)
• Real markets may behave differently than models predict

Transaction Costs

• Frequent rebalancing incurs commissions and bid-ask spreads
• These costs can significantly reduce profitability of hedging strategies

Liquidity Issues

• Some options have wide bid-ask spreads or low volume
• This makes precise hedging difficult or costly

Volatility Smile and Skew

• In reality, implied volatility varies across strike prices
• OTM puts often have higher implied volatility (volatility skew)
• This affects how Greeks behave across different strikes

Discrete Hedging vs. Continuous Models

• Models assume continuous hedging
• Real-world hedging happens at discrete intervals
• This gap creates additional risk

Conclusion

Understanding Options Greeks transforms complex option dynamics into manageable risk metrics:

• Delta quantifies directional exposure
• Gamma indicates the stability of that exposure
• Theta represents time decay cost/benefit
• Vega measures volatility sensitivity
• Rho accounts for interest rate impact

By monitoring these Greeks and understanding their relationships, traders can:

• Create more sophisticated strategies beyond simple directional bets
• Better manage risk across their portfolio
• Make more informed decisions about entry, exit, and adjustment points

Remember that Greeks are guides, not guarantees. Successful options trading requires continuous learning, disciplined risk management, and adaptation to changing market conditions.